engine/src/flutter/lib/ui/geometry.dart

// Copyright 2013 The Flutter Authors. All rights reserved.
// Use of this source code is governed by a BSD-style license that can be
// found in the LICENSE file.

part of dart.ui;

/// Base class for [Size] and [Offset], which are both ways to describe
/// a distance as a two-dimensional axis-aligned vector.
abstract class OffsetBase {
  /// Abstract const constructor. This constructor enables subclasses to provide
  /// const constructors so that they can be used in const expressions.
  ///
  /// The first argument sets the horizontal component, and the second the
  /// vertical component.
  const OffsetBase(this._dx, this._dy);

  final double _dx;
  final double _dy;

  /// Returns true if either component is [double.infinity], and false if both
  /// are finite (or negative infinity, or NaN).
  ///
  /// This is different than comparing for equality with an instance that has
  /// _both_ components set to [double.infinity].
  ///
  /// See also:
  ///
  ///  * [isFinite], which is true if both components are finite (and not NaN).
  bool get isInfinite => _dx >= double.infinity || _dy >= double.infinity;

  /// Whether both components are finite (neither infinite nor NaN).
  ///
  /// See also:
  ///
  ///  * [isInfinite], which returns true if either component is equal to
  ///    positive infinity.
  bool get isFinite => _dx.isFinite && _dy.isFinite;

  /// Less-than operator. Compares an [Offset] or [Size] to another [Offset] or
  /// [Size], and returns true if both the horizontal and vertical values of the
  /// left-hand-side operand are smaller than the horizontal and vertical values
  /// of the right-hand-side operand respectively. Returns false otherwise.
  ///
  /// This is a partial ordering. It is possible for two values to be neither
  /// less, nor greater than, nor equal to, another.
  bool operator <(OffsetBase other) => _dx < other._dx && _dy < other._dy;

  /// Less-than-or-equal-to operator. Compares an [Offset] or [Size] to another
  /// [Offset] or [Size], and returns true if both the horizontal and vertical
  /// values of the left-hand-side operand are smaller than or equal to the
  /// horizontal and vertical values of the right-hand-side operand
  /// respectively. Returns false otherwise.
  ///
  /// This is a partial ordering. It is possible for two values to be neither
  /// less, nor greater than, nor equal to, another.
  bool operator <=(OffsetBase other) => _dx <= other._dx && _dy <= other._dy;

  /// Greater-than operator. Compares an [Offset] or [Size] to another [Offset]
  /// or [Size], and returns true if both the horizontal and vertical values of
  /// the left-hand-side operand are bigger than the horizontal and vertical
  /// values of the right-hand-side operand respectively. Returns false
  /// otherwise.
  ///
  /// This is a partial ordering. It is possible for two values to be neither
  /// less, nor greater than, nor equal to, another.
  bool operator >(OffsetBase other) => _dx > other._dx && _dy > other._dy;

  /// Greater-than-or-equal-to operator. Compares an [Offset] or [Size] to
  /// another [Offset] or [Size], and returns true if both the horizontal and
  /// vertical values of the left-hand-side operand are bigger than or equal to
  /// the horizontal and vertical values of the right-hand-side operand
  /// respectively. Returns false otherwise.
  ///
  /// This is a partial ordering. It is possible for two values to be neither
  /// less, nor greater than, nor equal to, another.
  bool operator >=(OffsetBase other) => _dx >= other._dx && _dy >= other._dy;

  /// Equality operator. Compares an [Offset] or [Size] to another [Offset] or
  /// [Size], and returns true if the horizontal and vertical values of the
  /// left-hand-side operand are equal to the horizontal and vertical values of
  /// the right-hand-side operand respectively. Returns false otherwise.
  @override
  bool operator ==(Object other) {
    return other is OffsetBase && other._dx == _dx && other._dy == _dy;
  }

  @override
  int get hashCode => Object.hash(_dx, _dy);

  @override
  String toString() => 'OffsetBase(${_dx.toStringAsFixed(1)}, ${_dy.toStringAsFixed(1)})';
}

/// An immutable 2D floating-point offset.
///
/// Generally speaking, Offsets can be interpreted in two ways:
///
/// 1. As representing a point in Cartesian space a specified distance from a
///    separately-maintained origin. For example, the top-left position of
///    children in the [RenderBox] protocol is typically represented as an
///    [Offset] from the top left of the parent box.
///
/// 2. As a vector that can be applied to coordinates. For example, when
///    painting a [RenderObject], the parent is passed an [Offset] from the
///    screen's origin which it can add to the offsets of its children to find
///    the [Offset] from the screen's origin to each of the children.
///
/// Because a particular [Offset] can be interpreted as one sense at one time
/// then as the other sense at a later time, the same class is used for both
/// senses.
///
/// See also:
///
///  * [Size], which represents a vector describing the size of a rectangle.
class Offset extends OffsetBase {
  /// Creates an offset. The first argument sets [dx], the horizontal component,
  /// and the second sets [dy], the vertical component.
  const Offset(super.dx, super.dy);

  /// Creates an offset from its [direction] and [distance].
  ///
  /// The direction is in radians clockwise from the positive x-axis.
  ///
  /// The distance can be omitted, to create a unit vector (distance = 1.0).
  factory Offset.fromDirection(double direction, [double distance = 1.0]) {
    return Offset(distance * math.cos(direction), distance * math.sin(direction));
  }

  /// The x component of the offset.
  ///
  /// The y component is given by [dy].
  double get dx => _dx;

  /// The y component of the offset.
  ///
  /// The x component is given by [dx].
  double get dy => _dy;

  /// The magnitude of the offset.
  ///
  /// If you need this value to compare it to another [Offset]'s distance,
  /// consider using [distanceSquared] instead, since it is cheaper to compute.
  double get distance => math.sqrt(dx * dx + dy * dy);

  /// The square of the magnitude of the offset.
  ///
  /// This is cheaper than computing the [distance] itself.
  double get distanceSquared => dx * dx + dy * dy;

  /// The angle of this offset as radians clockwise from the positive x-axis, in
  /// the range -[pi] to [pi], assuming positive values of the x-axis go to the
  /// right and positive values of the y-axis go down.
  ///
  /// Zero means that [dy] is zero and [dx] is zero or positive.
  ///
  /// Values from zero to [pi]/2 indicate positive values of [dx] and [dy], the
  /// bottom-right quadrant.
  ///
  /// Values from [pi]/2 to [pi] indicate negative values of [dx] and positive
  /// values of [dy], the bottom-left quadrant.
  ///
  /// Values from zero to -[pi]/2 indicate positive values of [dx] and negative
  /// values of [dy], the top-right quadrant.
  ///
  /// Values from -[pi]/2 to -[pi] indicate negative values of [dx] and [dy],
  /// the top-left quadrant.
  ///
  /// When [dy] is zero and [dx] is negative, the [direction] is [pi].
  ///
  /// When [dx] is zero, [direction] is [pi]/2 if [dy] is positive and -[pi]/2
  /// if [dy] is negative.
  ///
  /// See also:
  ///
  ///  * [distance], to compute the magnitude of the vector.
  ///  * [Canvas.rotate], which uses the same convention for its angle.
  double get direction => math.atan2(dy, dx);

  /// An offset with zero magnitude.
  ///
  /// This can be used to represent the origin of a coordinate space.
  static const Offset zero = Offset(0.0, 0.0);

  /// An offset with infinite x and y components.
  ///
  /// See also:
  ///
  ///  * [isInfinite], which checks whether either component is infinite.
  ///  * [isFinite], which checks whether both components are finite.
  // This is included for completeness, because [Size.infinite] exists.
  static const Offset infinite = Offset(double.infinity, double.infinity);

  /// Returns a new offset with the x component scaled by `scaleX` and the y
  /// component scaled by `scaleY`.
  ///
  /// If the two scale arguments are the same, consider using the `*` operator
  /// instead:
  ///
  /// ```dart
  /// Offset a = const Offset(10.0, 10.0);
  /// Offset b = a * 2.0; // same as: a.scale(2.0, 2.0)
  /// ```
  ///
  /// If the two arguments are -1, consider using the unary `-` operator
  /// instead:
  ///
  /// ```dart
  /// Offset a = const Offset(10.0, 10.0);
  /// Offset b = -a; // same as: a.scale(-1.0, -1.0)
  /// ```
  Offset scale(double scaleX, double scaleY) => Offset(dx * scaleX, dy * scaleY);

  /// Returns a new offset with translateX added to the x component and
  /// translateY added to the y component.
  ///
  /// If the arguments come from another [Offset], consider using the `+` or `-`
  /// operators instead:
  ///
  /// ```dart
  /// Offset a = const Offset(10.0, 10.0);
  /// Offset b = const Offset(10.0, 10.0);
  /// Offset c = a + b; // same as: a.translate(b.dx, b.dy)
  /// Offset d = a - b; // same as: a.translate(-b.dx, -b.dy)
  /// ```
  Offset translate(double translateX, double translateY) =>
      Offset(dx + translateX, dy + translateY);

  /// Unary negation operator.
  ///
  /// Returns an offset with the coordinates negated.
  ///
  /// If the [Offset] represents an arrow on a plane, this operator returns the
  /// same arrow but pointing in the reverse direction.
  Offset operator -() => Offset(-dx, -dy);

  /// Binary subtraction operator.
  ///
  /// Returns an offset whose [dx] value is the left-hand-side operand's [dx]
  /// minus the right-hand-side operand's [dx] and whose [dy] value is the
  /// left-hand-side operand's [dy] minus the right-hand-side operand's [dy].
  ///
  /// See also [translate].
  Offset operator -(Offset other) => Offset(dx - other.dx, dy - other.dy);

  /// Binary addition operator.
  ///
  /// Returns an offset whose [dx] value is the sum of the [dx] values of the
  /// two operands, and whose [dy] value is the sum of the [dy] values of the
  /// two operands.
  ///
  /// See also [translate].
  Offset operator +(Offset other) => Offset(dx + other.dx, dy + other.dy);

  /// Multiplication operator.
  ///
  /// Returns an offset whose coordinates are the coordinates of the
  /// left-hand-side operand (an Offset) multiplied by the scalar
  /// right-hand-side operand (a double).
  ///
  /// See also [scale].
  Offset operator *(double operand) => Offset(dx * operand, dy * operand);

  /// Division operator.
  ///
  /// Returns an offset whose coordinates are the coordinates of the
  /// left-hand-side operand (an Offset) divided by the scalar right-hand-side
  /// operand (a double).
  ///
  /// See also [scale].
  Offset operator /(double operand) => Offset(dx / operand, dy / operand);

  /// Integer (truncating) division operator.
  ///
  /// Returns an offset whose coordinates are the coordinates of the
  /// left-hand-side operand (an Offset) divided by the scalar right-hand-side
  /// operand (a double), rounded towards zero.
  Offset operator ~/(double operand) =>
      Offset((dx ~/ operand).toDouble(), (dy ~/ operand).toDouble());

  /// Modulo (remainder) operator.
  ///
  /// Returns an offset whose coordinates are the remainder of dividing the
  /// coordinates of the left-hand-side operand (an Offset) by the scalar
  /// right-hand-side operand (a double).
  Offset operator %(double operand) => Offset(dx % operand, dy % operand);

  /// Rectangle constructor operator.
  ///
  /// Combines an [Offset] and a [Size] to form a [Rect] whose top-left
  /// coordinate is the point given by adding this offset, the left-hand-side
  /// operand, to the origin, and whose size is the right-hand-side operand.
  ///
  /// ```dart
  /// Rect myRect = Offset.zero & const Size(100.0, 100.0);
  /// // same as: Rect.fromLTWH(0.0, 0.0, 100.0, 100.0)
  /// ```
  Rect operator &(Size other) => Rect.fromLTWH(dx, dy, other.width, other.height);

  /// Linearly interpolate between two offsets.
  ///
  /// If either offset is null, this function interpolates from [Offset.zero].
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static Offset? lerp(Offset? a, Offset? b, double t) {
    if (b == null) {
      if (a == null) {
        return null;
      } else {
        return a * (1.0 - t);
      }
    } else {
      if (a == null) {
        return b * t;
      } else {
        return Offset(_lerpDouble(a.dx, b.dx, t), _lerpDouble(a.dy, b.dy, t));
      }
    }
  }

  /// Compares two Offsets for equality.
  @override
  bool operator ==(Object other) {
    return other is Offset && other.dx == dx && other.dy == dy;
  }

  @override
  int get hashCode => Object.hash(dx, dy);

  @override
  String toString() => 'Offset(${dx.toStringAsFixed(1)}, ${dy.toStringAsFixed(1)})';
}

/// Holds a 2D floating-point size.
///
/// You can think of this as an [Offset] from the origin.
class Size extends OffsetBase {
  /// Creates a [Size] with the given [width] and [height].
  const Size(super.width, super.height);

  /// Creates an instance of [Size] that has the same values as another.
  // Used by the rendering library's _DebugSize hack.
  Size.copy(Size source) : super(source.width, source.height);

  /// Creates a square [Size] whose [width] and [height] are the given dimension.
  ///
  /// See also:
  ///
  ///  * [Size.fromRadius], which is more convenient when the available size
  ///    is the radius of a circle.
  const Size.square(double dimension) : super(dimension, dimension);

  /// Creates a [Size] with the given [width] and an infinite [height].
  const Size.fromWidth(double width) : super(width, double.infinity);

  /// Creates a [Size] with the given [height] and an infinite [width].
  const Size.fromHeight(double height) : super(double.infinity, height);

  /// Creates a square [Size] whose [width] and [height] are twice the given
  /// dimension.
  ///
  /// This is a square that contains a circle with the given radius.
  ///
  /// See also:
  ///
  ///  * [Size.square], which creates a square with the given dimension.
  const Size.fromRadius(double radius) : super(radius * 2.0, radius * 2.0);

  /// The horizontal extent of this size.
  double get width => _dx;

  /// The vertical extent of this size.
  double get height => _dy;

  /// The aspect ratio of this size.
  ///
  /// This returns the [width] divided by the [height].
  ///
  /// If the [width] is zero, the result will be zero. If the [height] is zero
  /// (and the [width] is not), the result will be [double.infinity] or
  /// [double.negativeInfinity] as determined by the sign of [width].
  ///
  /// See also:
  ///
  ///  * [AspectRatio], a widget for giving a child widget a specific aspect
  ///    ratio.
  ///  * [FittedBox], a widget that (in most modes) attempts to maintain a
  ///    child widget's aspect ratio while changing its size.
  double get aspectRatio {
    if (height != 0.0) {
      return width / height;
    }
    if (width > 0.0) {
      return double.infinity;
    }
    if (width < 0.0) {
      return double.negativeInfinity;
    }
    return 0.0;
  }

  /// An empty size, one with a zero width and a zero height.
  static const Size zero = Size(0.0, 0.0);

  /// A size whose [width] and [height] are infinite.
  ///
  /// See also:
  ///
  ///  * [isInfinite], which checks whether either dimension is infinite.
  ///  * [isFinite], which checks whether both dimensions are finite.
  static const Size infinite = Size(double.infinity, double.infinity);

  /// Whether this size encloses a non-zero area.
  ///
  /// Negative areas are considered empty.
  bool get isEmpty => width <= 0.0 || height <= 0.0;

  /// Binary subtraction operator for [Size].
  ///
  /// Subtracting a [Size] from a [Size] returns the [Offset] that describes how
  /// much bigger the left-hand-side operand is than the right-hand-side
  /// operand. Adding that resulting [Offset] to the [Size] that was the
  /// right-hand-side operand would return a [Size] equal to the [Size] that was
  /// the left-hand-side operand. (i.e. if `sizeA - sizeB -> offsetA`, then
  /// `offsetA + sizeB -> sizeA`)
  ///
  /// Subtracting an [Offset] from a [Size] returns the [Size] that is smaller than
  /// the [Size] operand by the difference given by the [Offset] operand. In other
  /// words, the returned [Size] has a [width] consisting of the [width] of the
  /// left-hand-side operand minus the [Offset.dx] dimension of the
  /// right-hand-side operand, and a [height] consisting of the [height] of the
  /// left-hand-side operand minus the [Offset.dy] dimension of the
  /// right-hand-side operand.
  OffsetBase operator -(OffsetBase other) {
    if (other is Size) {
      return Offset(width - other.width, height - other.height);
    }
    if (other is Offset) {
      return Size(width - other.dx, height - other.dy);
    }
    throw ArgumentError(other);
  }

  /// Binary addition operator for adding an [Offset] to a [Size].
  ///
  /// Returns a [Size] whose [width] is the sum of the [width] of the
  /// left-hand-side operand, a [Size], and the [Offset.dx] dimension of the
  /// right-hand-side operand, an [Offset], and whose [height] is the sum of the
  /// [height] of the left-hand-side operand and the [Offset.dy] dimension of
  /// the right-hand-side operand.
  Size operator +(Offset other) => Size(width + other.dx, height + other.dy);

  /// Multiplication operator.
  ///
  /// Returns a [Size] whose dimensions are the dimensions of the left-hand-side
  /// operand (a [Size]) multiplied by the scalar right-hand-side operand (a
  /// [double]).
  Size operator *(double operand) => Size(width * operand, height * operand);

  /// Division operator.
  ///
  /// Returns a [Size] whose dimensions are the dimensions of the left-hand-side
  /// operand (a [Size]) divided by the scalar right-hand-side operand (a
  /// [double]).
  Size operator /(double operand) => Size(width / operand, height / operand);

  /// Integer (truncating) division operator.
  ///
  /// Returns a [Size] whose dimensions are the dimensions of the left-hand-side
  /// operand (a [Size]) divided by the scalar right-hand-side operand (a
  /// [double]), rounded towards zero.
  Size operator ~/(double operand) =>
      Size((width ~/ operand).toDouble(), (height ~/ operand).toDouble());

  /// Modulo (remainder) operator.
  ///
  /// Returns a [Size] whose dimensions are the remainder of dividing the
  /// left-hand-side operand (a [Size]) by the scalar right-hand-side operand (a
  /// [double]).
  Size operator %(double operand) => Size(width % operand, height % operand);

  /// The lesser of the magnitudes of the [width] and the [height].
  double get shortestSide => math.min(width.abs(), height.abs());

  /// The greater of the magnitudes of the [width] and the [height].
  double get longestSide => math.max(width.abs(), height.abs());

  // Convenience methods that do the equivalent of calling the similarly named
  // methods on a Rect constructed from the given origin and this size.

  /// The offset to the intersection of the top and left edges of the rectangle
  /// described by the given [Offset] (which is interpreted as the top-left corner)
  /// and this [Size].
  ///
  /// See also [Rect.topLeft].
  Offset topLeft(Offset origin) => origin;

  /// The offset to the center of the top edge of the rectangle described by the
  /// given offset (which is interpreted as the top-left corner) and this size.
  ///
  /// See also [Rect.topCenter].
  Offset topCenter(Offset origin) => Offset(origin.dx + width / 2.0, origin.dy);

  /// The offset to the intersection of the top and right edges of the rectangle
  /// described by the given offset (which is interpreted as the top-left corner)
  /// and this size.
  ///
  /// See also [Rect.topRight].
  Offset topRight(Offset origin) => Offset(origin.dx + width, origin.dy);

  /// The offset to the center of the left edge of the rectangle described by the
  /// given offset (which is interpreted as the top-left corner) and this size.
  ///
  /// See also [Rect.centerLeft].
  Offset centerLeft(Offset origin) => Offset(origin.dx, origin.dy + height / 2.0);

  /// The offset to the point halfway between the left and right and the top and
  /// bottom edges of the rectangle described by the given offset (which is
  /// interpreted as the top-left corner) and this size.
  ///
  /// See also [Rect.center].
  Offset center(Offset origin) => Offset(origin.dx + width / 2.0, origin.dy + height / 2.0);

  /// The offset to the center of the right edge of the rectangle described by the
  /// given offset (which is interpreted as the top-left corner) and this size.
  ///
  /// See also [Rect.centerRight].
  Offset centerRight(Offset origin) => Offset(origin.dx + width, origin.dy + height / 2.0);

  /// The offset to the intersection of the bottom and left edges of the
  /// rectangle described by the given offset (which is interpreted as the
  /// top-left corner) and this size.
  ///
  /// See also [Rect.bottomLeft].
  Offset bottomLeft(Offset origin) => Offset(origin.dx, origin.dy + height);

  /// The offset to the center of the bottom edge of the rectangle described by
  /// the given offset (which is interpreted as the top-left corner) and this
  /// size.
  ///
  /// See also [Rect.bottomCenter].
  Offset bottomCenter(Offset origin) => Offset(origin.dx + width / 2.0, origin.dy + height);

  /// The offset to the intersection of the bottom and right edges of the
  /// rectangle described by the given offset (which is interpreted as the
  /// top-left corner) and this size.
  ///
  /// See also [Rect.bottomRight].
  Offset bottomRight(Offset origin) => Offset(origin.dx + width, origin.dy + height);

  /// Whether the point specified by the given offset (which is assumed to be
  /// relative to the top left of the size) lies between the left and right and
  /// the top and bottom edges of a rectangle of this size.
  ///
  /// Rectangles include their top and left edges but exclude their bottom and
  /// right edges.
  bool contains(Offset offset) {
    return offset.dx >= 0.0 && offset.dx < width && offset.dy >= 0.0 && offset.dy < height;
  }

  /// A [Size] with the [width] and [height] swapped.
  Size get flipped => Size(height, width);

  /// Linearly interpolate between two sizes
  ///
  /// If either size is null, this function interpolates from [Size.zero].
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static Size? lerp(Size? a, Size? b, double t) {
    if (b == null) {
      if (a == null) {
        return null;
      } else {
        return a * (1.0 - t);
      }
    } else {
      if (a == null) {
        return b * t;
      } else {
        return Size(_lerpDouble(a.width, b.width, t), _lerpDouble(a.height, b.height, t));
      }
    }
  }

  /// Compares two Sizes for equality.
  // We don't compare the runtimeType because of _DebugSize in the framework.
  @override
  bool operator ==(Object other) {
    return other is Size && other._dx == _dx && other._dy == _dy;
  }

  @override
  int get hashCode => Object.hash(_dx, _dy);

  @override
  String toString() => 'Size(${width.toStringAsFixed(1)}, ${height.toStringAsFixed(1)})';
}

/// An immutable, 2D, axis-aligned, floating-point rectangle whose coordinates
/// are relative to a given origin.
///
/// A Rect can be created with one of its constructors or from an [Offset] and a
/// [Size] using the `&` operator:
///
/// ```dart
/// Rect myRect = const Offset(1.0, 2.0) & const Size(3.0, 4.0);
/// ```
class Rect {
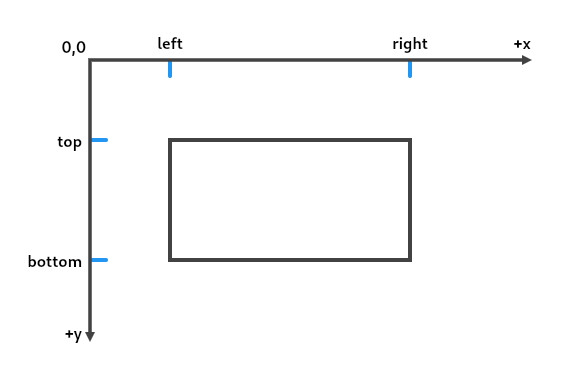
  /// Construct a rectangle from its left, top, right, and bottom edges.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_ltrb.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_ltrb_dark.png#gh-dark-mode-only)
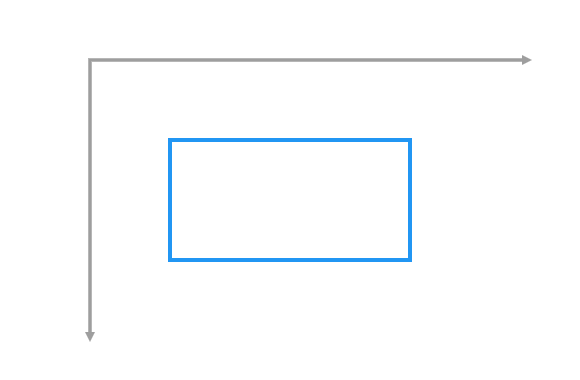  const Rect.fromLTRB(this.left, this.top, this.right, this.bottom);

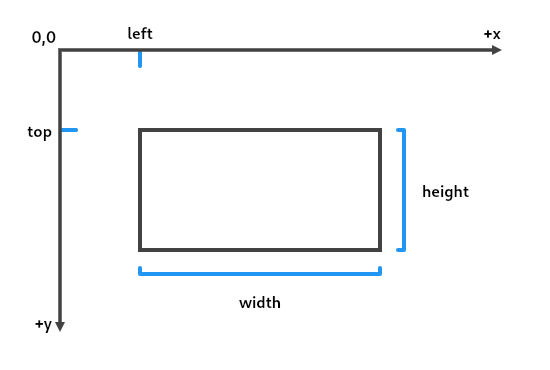
  /// Construct a rectangle from its left and top edges, its width, and its
  /// height.
  ///
  /// To construct a [Rect] from an [Offset] and a [Size], you can use the
  /// rectangle constructor operator `&`. See [Offset.&].
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_ltwh.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_ltwh_dark.png#gh-dark-mode-only)
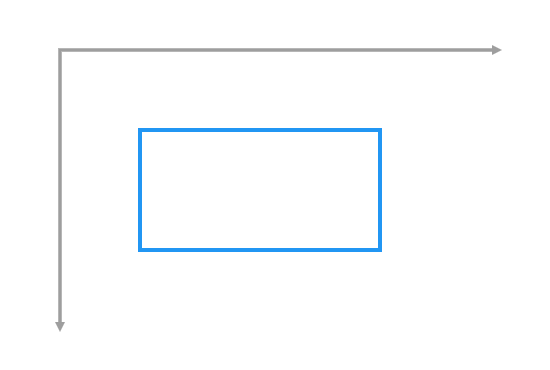  const Rect.fromLTWH(double left, double top, double width, double height)
    : this.fromLTRB(left, top, left + width, top + height);

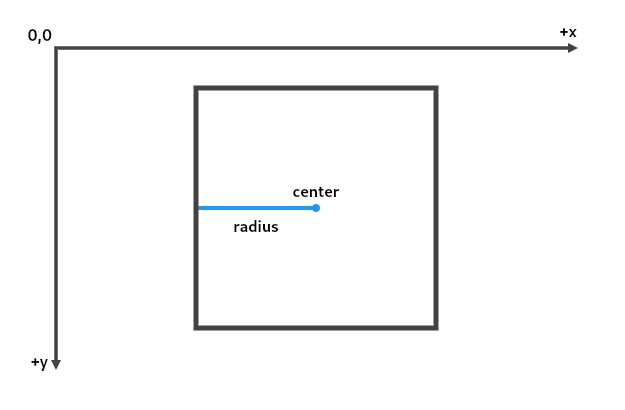
  /// Construct a rectangle that bounds the given circle.
  ///
  /// The `center` argument is assumed to be an offset from the origin.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_circle.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_circle_dark.png#gh-dark-mode-only)
  Rect.fromCircle({required Offset center, required double radius})
    : this.fromCenter(center: center, width: radius * 2, height: radius * 2);

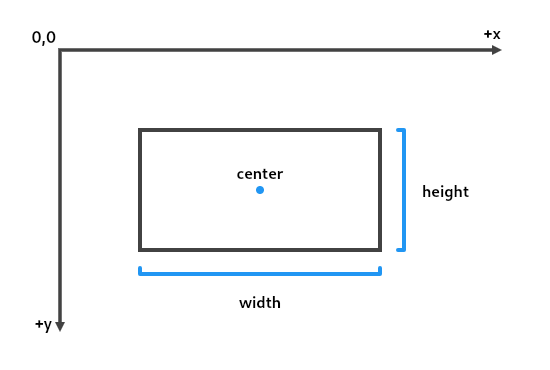
  /// Constructs a rectangle from its center point, width, and height.
  ///
  /// The `center` argument is assumed to be an offset from the origin.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_center.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_center_dark.png#gh-dark-mode-only)
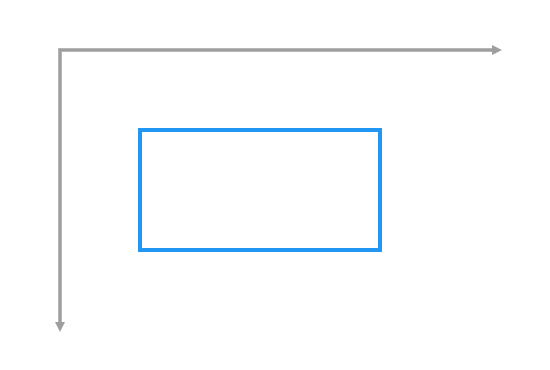  Rect.fromCenter({required Offset center, required double width, required double height})
    : this.fromLTRB(
        center.dx - width / 2,
        center.dy - height / 2,
        center.dx + width / 2,
        center.dy + height / 2,
      );

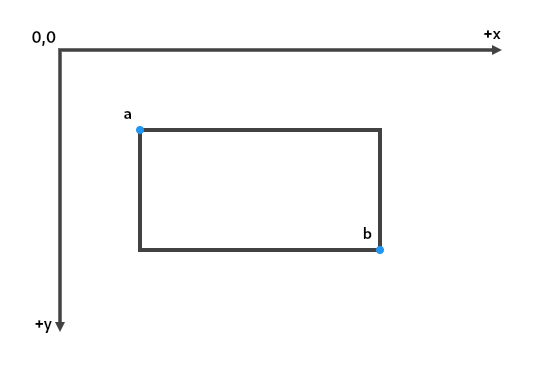
  /// Construct the smallest rectangle that encloses the given offsets, treating
  /// them as vectors from the origin.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_points.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/rect_from_points_dark.png#gh-dark-mode-only)
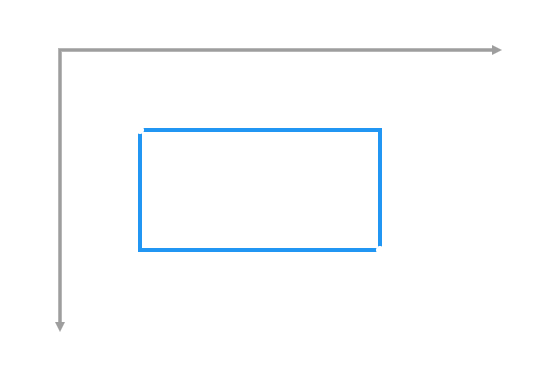  Rect.fromPoints(Offset a, Offset b)
    : this.fromLTRB(
        math.min(a.dx, b.dx),
        math.min(a.dy, b.dy),
        math.max(a.dx, b.dx),
        math.max(a.dy, b.dy),
      );

  Float32List _getValue32() {
    final Float32List result = Float32List(4);
    result[0] = left;
    result[1] = top;
    result[2] = right;
    result[3] = bottom;
    return result;
  }

  /// The offset of the left edge of this rectangle from the x axis.
  final double left;

  /// The offset of the top edge of this rectangle from the y axis.
  final double top;

  /// The offset of the right edge of this rectangle from the x axis.
  final double right;

  /// The offset of the bottom edge of this rectangle from the y axis.
  final double bottom;

  /// The distance between the left and right edges of this rectangle.
  double get width => right - left;

  /// The distance between the top and bottom edges of this rectangle.
  double get height => bottom - top;

  /// The distance between the upper-left corner and the lower-right corner of
  /// this rectangle.
  Size get size => Size(width, height);

  /// Whether any of the dimensions are `NaN`.
  bool get hasNaN => left.isNaN || top.isNaN || right.isNaN || bottom.isNaN;

  /// A rectangle with left, top, right, and bottom edges all at zero.
  static const Rect zero = Rect.fromLTRB(0.0, 0.0, 0.0, 0.0);

  static const double _giantScalar = 1.0E+9; // matches kGiantRect from layer.h

  /// A rectangle that covers the entire coordinate space.
  ///
  /// This covers the space from -1e9,-1e9 to 1e9,1e9.
  /// This is the space over which graphics operations are valid.
  static const Rect largest = Rect.fromLTRB(
    -_giantScalar,
    -_giantScalar,
    _giantScalar,
    _giantScalar,
  );

  /// Whether any of the coordinates of this rectangle are equal to positive infinity.
  // included for consistency with Offset and Size
  bool get isInfinite {
    return left >= double.infinity ||
        top >= double.infinity ||
        right >= double.infinity ||
        bottom >= double.infinity;
  }

  /// Whether all coordinates of this rectangle are finite.
  bool get isFinite => left.isFinite && top.isFinite && right.isFinite && bottom.isFinite;

  /// Whether this rectangle encloses a non-zero area. Negative areas are
  /// considered empty.
  bool get isEmpty => left >= right || top >= bottom;

  /// Returns a new rectangle translated by the given offset.
  ///
  /// To translate a rectangle by separate x and y components rather than by an
  /// [Offset], consider [translate].
  Rect shift(Offset offset) {
    return Rect.fromLTRB(left + offset.dx, top + offset.dy, right + offset.dx, bottom + offset.dy);
  }

  /// Returns a new rectangle with translateX added to the x components and
  /// translateY added to the y components.
  ///
  /// To translate a rectangle by an [Offset] rather than by separate x and y
  /// components, consider [shift].
  Rect translate(double translateX, double translateY) {
    return Rect.fromLTRB(
      left + translateX,
      top + translateY,
      right + translateX,
      bottom + translateY,
    );
  }

  /// Returns a new rectangle with edges moved outwards by the given delta.
  Rect inflate(double delta) {
    return Rect.fromLTRB(left - delta, top - delta, right + delta, bottom + delta);
  }

  /// Returns a new rectangle with edges moved inwards by the given delta.
  Rect deflate(double delta) => inflate(-delta);

  /// Returns a new rectangle that is the intersection of the given
  /// rectangle and this rectangle. The two rectangles must overlap
  /// for this to be meaningful. If the two rectangles do not overlap,
  /// then the resulting Rect will have a negative width or height.
  Rect intersect(Rect other) {
    return Rect.fromLTRB(
      math.max(left, other.left),
      math.max(top, other.top),
      math.min(right, other.right),
      math.min(bottom, other.bottom),
    );
  }

  /// Returns a new rectangle which is the bounding box containing this
  /// rectangle and the given rectangle.
  Rect expandToInclude(Rect other) {
    return Rect.fromLTRB(
      math.min(left, other.left),
      math.min(top, other.top),
      math.max(right, other.right),
      math.max(bottom, other.bottom),
    );
  }

  /// Whether `other` has a nonzero area of overlap with this rectangle.
  bool overlaps(Rect other) {
    if (right <= other.left || other.right <= left) {
      return false;
    }
    if (bottom <= other.top || other.bottom <= top) {
      return false;
    }
    return true;
  }

  /// The lesser of the magnitudes of the [width] and the [height] of this
  /// rectangle.
  double get shortestSide => math.min(width.abs(), height.abs());

  /// The greater of the magnitudes of the [width] and the [height] of this
  /// rectangle.
  double get longestSide => math.max(width.abs(), height.abs());

  /// The offset to the intersection of the top and left edges of this rectangle.
  ///
  /// See also [Size.topLeft].
  Offset get topLeft => Offset(left, top);

  /// The offset to the center of the top edge of this rectangle.
  ///
  /// See also [Size.topCenter].
  Offset get topCenter => Offset(left + width / 2.0, top);

  /// The offset to the intersection of the top and right edges of this rectangle.
  ///
  /// See also [Size.topRight].
  Offset get topRight => Offset(right, top);

  /// The offset to the center of the left edge of this rectangle.
  ///
  /// See also [Size.centerLeft].
  Offset get centerLeft => Offset(left, top + height / 2.0);

  /// The offset to the point halfway between the left and right and the top and
  /// bottom edges of this rectangle.
  ///
  /// See also [Size.center].
  Offset get center => Offset(left + width / 2.0, top + height / 2.0);

  /// The offset to the center of the right edge of this rectangle.
  ///
  /// See also [Size.centerRight].
  Offset get centerRight => Offset(right, top + height / 2.0);

  /// The offset to the intersection of the bottom and left edges of this rectangle.
  ///
  /// See also [Size.bottomLeft].
  Offset get bottomLeft => Offset(left, bottom);

  /// The offset to the center of the bottom edge of this rectangle.
  ///
  /// See also [Size.bottomCenter].
  Offset get bottomCenter => Offset(left + width / 2.0, bottom);

  /// The offset to the intersection of the bottom and right edges of this rectangle.
  ///
  /// See also [Size.bottomRight].
  Offset get bottomRight => Offset(right, bottom);

  /// Whether the point specified by the given offset (which is assumed to be
  /// relative to the origin) lies between the left and right and the top and
  /// bottom edges of this rectangle.
  ///
  /// Rectangles include their top and left edges but exclude their bottom and
  /// right edges.
  bool contains(Offset offset) {
    return offset.dx >= left && offset.dx < right && offset.dy >= top && offset.dy < bottom;
  }

  /// Linearly interpolate between two rectangles.
  ///
  /// If either rect is null, [Rect.zero] is used as a substitute.
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static Rect? lerp(Rect? a, Rect? b, double t) {
    if (b == null) {
      if (a == null) {
        return null;
      } else {
        final double k = 1.0 - t;
        return Rect.fromLTRB(a.left * k, a.top * k, a.right * k, a.bottom * k);
      }
    } else {
      if (a == null) {
        return Rect.fromLTRB(b.left * t, b.top * t, b.right * t, b.bottom * t);
      } else {
        return Rect.fromLTRB(
          _lerpDouble(a.left, b.left, t),
          _lerpDouble(a.top, b.top, t),
          _lerpDouble(a.right, b.right, t),
          _lerpDouble(a.bottom, b.bottom, t),
        );
      }
    }
  }

  @override
  bool operator ==(Object other) {
    if (identical(this, other)) {
      return true;
    }
    if (runtimeType != other.runtimeType) {
      return false;
    }
    return other is Rect &&
        other.left == left &&
        other.top == top &&
        other.right == right &&
        other.bottom == bottom;
  }

  @override
  int get hashCode => Object.hash(left, top, right, bottom);

  @override
  String toString() =>
      'Rect.fromLTRB(${left.toStringAsFixed(1)}, ${top.toStringAsFixed(1)}, ${right.toStringAsFixed(1)}, ${bottom.toStringAsFixed(1)})';
}

/// A radius for either circular or elliptical shapes.
class Radius {
  /// Constructs a circular radius. [x] and [y] will have the same radius value.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/radius_circular.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/radius_circular_dark.png#gh-dark-mode-only)
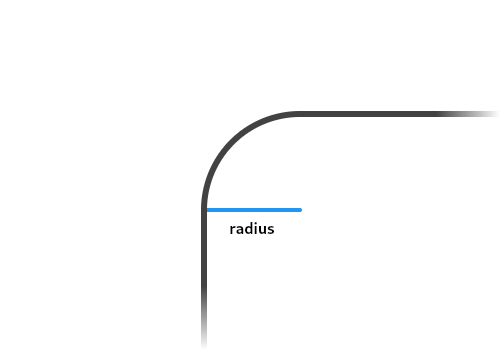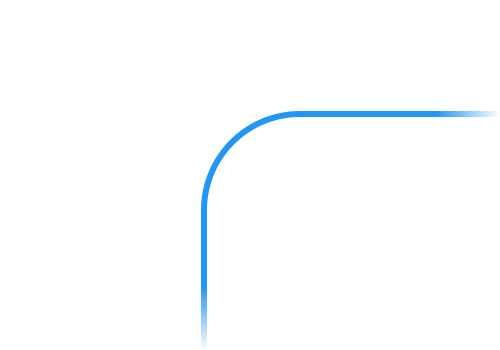  const Radius.circular(double radius) : this.elliptical(radius, radius);

  /// Constructs an elliptical radius with the given radii.
  ///
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/radius_elliptical.png#gh-light-mode-only)
  /// ![](https://flutter.github.io/assets-for-api-docs/assets/dart-ui/radius_elliptical_dark.png#gh-dark-mode-only)
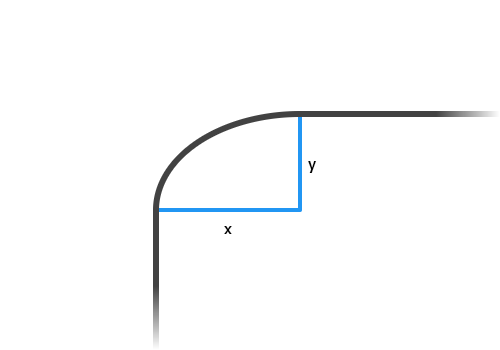  const Radius.elliptical(this.x, this.y);

  /// The radius value on the horizontal axis.
  final double x;

  /// The radius value on the vertical axis.
  final double y;

  /// A radius with [x] and [y] values set to zero.
  ///
  /// You can use [Radius.zero] with [RRect] or [RSuperellipse] to have
  /// right-angle corners.
  static const Radius zero = Radius.circular(0.0);

  /// Returns this [Radius], with values clamped to the given min and max
  /// [Radius] values.
  ///
  /// The `min` value defaults to `Radius.circular(-double.infinity)`, and
  /// the `max` value defaults to `Radius.circular(double.infinity)`.
  Radius clamp({Radius? minimum, Radius? maximum}) {
    minimum ??= const Radius.circular(-double.infinity);
    maximum ??= const Radius.circular(double.infinity);
    return Radius.elliptical(
      clampDouble(x, minimum.x, maximum.x),
      clampDouble(y, minimum.y, maximum.y),
    );
  }

  /// Returns this [Radius], with values clamped to the given min and max
  /// values in each dimension
  ///
  /// The `minimumX` and `minimumY` values default to `-double.infinity`, and
  /// the `maximumX` and `maximumY` values default to `double.infinity`.
  Radius clampValues({double? minimumX, double? minimumY, double? maximumX, double? maximumY}) {
    return Radius.elliptical(
      clampDouble(x, minimumX ?? -double.infinity, maximumX ?? double.infinity),
      clampDouble(y, minimumY ?? -double.infinity, maximumY ?? double.infinity),
    );
  }

  /// Unary negation operator.
  ///
  /// Returns a Radius with the distances negated.
  ///
  /// Radiuses with negative values aren't geometrically meaningful, but could
  /// occur as part of expressions. For example, negating a radius of one pixel
  /// and then adding the result to another radius is equivalent to subtracting
  /// a radius of one pixel from the other.
  Radius operator -() => Radius.elliptical(-x, -y);

  /// Binary subtraction operator.
  ///
  /// Returns a radius whose [x] value is the left-hand-side operand's [x]
  /// minus the right-hand-side operand's [x] and whose [y] value is the
  /// left-hand-side operand's [y] minus the right-hand-side operand's [y].
  Radius operator -(Radius other) => Radius.elliptical(x - other.x, y - other.y);

  /// Binary addition operator.
  ///
  /// Returns a radius whose [x] value is the sum of the [x] values of the
  /// two operands, and whose [y] value is the sum of the [y] values of the
  /// two operands.
  Radius operator +(Radius other) => Radius.elliptical(x + other.x, y + other.y);

  /// Multiplication operator.
  ///
  /// Returns a radius whose coordinates are the coordinates of the
  /// left-hand-side operand (a radius) multiplied by the scalar
  /// right-hand-side operand (a double).
  Radius operator *(double operand) => Radius.elliptical(x * operand, y * operand);

  /// Division operator.
  ///
  /// Returns a radius whose coordinates are the coordinates of the
  /// left-hand-side operand (a radius) divided by the scalar right-hand-side
  /// operand (a double).
  Radius operator /(double operand) => Radius.elliptical(x / operand, y / operand);

  /// Integer (truncating) division operator.
  ///
  /// Returns a radius whose coordinates are the coordinates of the
  /// left-hand-side operand (a radius) divided by the scalar right-hand-side
  /// operand (a double), rounded towards zero.
  Radius operator ~/(double operand) =>
      Radius.elliptical((x ~/ operand).toDouble(), (y ~/ operand).toDouble());

  /// Modulo (remainder) operator.
  ///
  /// Returns a radius whose coordinates are the remainder of dividing the
  /// coordinates of the left-hand-side operand (a radius) by the scalar
  /// right-hand-side operand (a double).
  Radius operator %(double operand) => Radius.elliptical(x % operand, y % operand);

  /// Linearly interpolate between two radii.
  ///
  /// If either is null, this function substitutes [Radius.zero] instead.
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static Radius? lerp(Radius? a, Radius? b, double t) {
    if (b == null) {
      if (a == null) {
        return null;
      } else {
        final double k = 1.0 - t;
        return Radius.elliptical(a.x * k, a.y * k);
      }
    } else {
      if (a == null) {
        return Radius.elliptical(b.x * t, b.y * t);
      } else {
        return Radius.elliptical(_lerpDouble(a.x, b.x, t), _lerpDouble(a.y, b.y, t));
      }
    }
  }

  @override
  bool operator ==(Object other) {
    if (identical(this, other)) {
      return true;
    }
    if (runtimeType != other.runtimeType) {
      return false;
    }

    return other is Radius && other.x == x && other.y == y;
  }

  @override
  int get hashCode => Object.hash(x, y);

  @override
  String toString() {
    return x == y
        ? 'Radius.circular(${x.toStringAsFixed(1)})'
        : 'Radius.elliptical(${x.toStringAsFixed(1)}, '
            '${y.toStringAsFixed(1)})';
  }
}

// The common base class for `RRect` and `RSuperellipse`.
abstract class _RRectLike<T extends _RRectLike<T>> {
  const _RRectLike({
    required this.left,
    required this.top,
    required this.right,
    required this.bottom,
    required this.tlRadiusX,
    required this.tlRadiusY,
    required this.trRadiusX,
    required this.trRadiusY,
    required this.brRadiusX,
    required this.brRadiusY,
    required this.blRadiusX,
    required this.blRadiusY,
  }) : assert(tlRadiusX >= 0),
       assert(tlRadiusY >= 0),
       assert(trRadiusX >= 0),
       assert(trRadiusY >= 0),
       assert(brRadiusX >= 0),
       assert(brRadiusY >= 0),
       assert(blRadiusX >= 0),
       assert(blRadiusY >= 0);

  // Implemented by a subclass to return an object constructed with the given
  // parameters.
  //
  // Used by various methods that construct an object of the same shape.
  T _create({
    required double left,
    required double top,
    required double right,
    required double bottom,
    required double tlRadiusX,
    required double tlRadiusY,
    required double trRadiusX,
    required double trRadiusY,
    required double brRadiusX,
    required double brRadiusY,
    required double blRadiusX,
    required double blRadiusY,
  });

  /// The offset of the left edge of this rectangle from the x axis.
  final double left;

  /// The offset of the top edge of this rectangle from the y axis.
  final double top;

  /// The offset of the right edge of this rectangle from the x axis.
  final double right;

  /// The offset of the bottom edge of this rectangle from the y axis.
  final double bottom;

  /// The top-left horizontal radius.
  final double tlRadiusX;

  /// The top-left vertical radius.
  final double tlRadiusY;

  /// The top-left [Radius].
  Radius get tlRadius => Radius.elliptical(tlRadiusX, tlRadiusY);

  /// The top-right horizontal radius.
  final double trRadiusX;

  /// The top-right vertical radius.
  final double trRadiusY;

  /// The top-right [Radius].
  Radius get trRadius => Radius.elliptical(trRadiusX, trRadiusY);

  /// The bottom-right horizontal radius.
  final double brRadiusX;

  /// The bottom-right vertical radius.
  final double brRadiusY;

  /// The bottom-right [Radius].
  Radius get brRadius => Radius.elliptical(brRadiusX, brRadiusY);

  /// The bottom-left horizontal radius.
  final double blRadiusX;

  /// The bottom-left vertical radius.
  final double blRadiusY;

  /// The bottom-left [Radius].
  Radius get blRadius => Radius.elliptical(blRadiusX, blRadiusY);

  /// Returns a clone translated by the given offset.
  T shift(Offset offset) {
    return _create(
      left: left + offset.dx,
      top: top + offset.dy,
      right: right + offset.dx,
      bottom: bottom + offset.dy,
      tlRadiusX: tlRadiusX,
      tlRadiusY: tlRadiusY,
      trRadiusX: trRadiusX,
      trRadiusY: trRadiusY,
      blRadiusX: blRadiusX,
      blRadiusY: blRadiusY,
      brRadiusX: brRadiusX,
      brRadiusY: brRadiusY,
    );
  }

  /// Returns a clone with edges and radii moved outwards by the given
  /// delta.
  T inflate(double delta) {
    return _create(
      left: left - delta,
      top: top - delta,
      right: right + delta,
      bottom: bottom + delta,
      tlRadiusX: math.max(0, tlRadiusX + delta),
      tlRadiusY: math.max(0, tlRadiusY + delta),
      trRadiusX: math.max(0, trRadiusX + delta),
      trRadiusY: math.max(0, trRadiusY + delta),
      blRadiusX: math.max(0, blRadiusX + delta),
      blRadiusY: math.max(0, blRadiusY + delta),
      brRadiusX: math.max(0, brRadiusX + delta),
      brRadiusY: math.max(0, brRadiusY + delta),
    );
  }

  /// Returns a clone with edges and radii moved inwards by the given delta.
  T deflate(double delta) => inflate(-delta);

  /// The distance between the left and right edges of this rectangle.
  double get width => right - left;

  /// The distance between the top and bottom edges of this rectangle.
  double get height => bottom - top;

  /// The bounding box of this rounded rectangle (the rectangle with no rounded corners).
  Rect get outerRect => Rect.fromLTRB(left, top, right, bottom);

  /// The non-rounded rectangle that is constrained by the smaller of the two
  /// diagonals, with each diagonal traveling through the middle of the curve
  /// corners. The middle of a corner is the intersection of the curve with its
  /// respective quadrant bisector.
  Rect get safeInnerRect {
    const double kInsetFactor = 0.29289321881; // 1-cos(pi/4)

    final double leftRadius = math.max(blRadiusX, tlRadiusX);
    final double topRadius = math.max(tlRadiusY, trRadiusY);
    final double rightRadius = math.max(trRadiusX, brRadiusX);
    final double bottomRadius = math.max(brRadiusY, blRadiusY);

    return Rect.fromLTRB(
      left + leftRadius * kInsetFactor,
      top + topRadius * kInsetFactor,
      right - rightRadius * kInsetFactor,
      bottom - bottomRadius * kInsetFactor,
    );
  }

  /// The rectangle that would be formed using the axis-aligned intersection of
  /// the sides of the rectangle, i.e., the rectangle formed from the
  /// inner-most centers of the ellipses that form the corners. This is the
  /// intersection of the [wideMiddleRect] and the [tallMiddleRect]. If any of
  /// the intersections are void, the resulting [Rect] will have negative width
  /// or height.
  Rect get middleRect {
    final double leftRadius = math.max(blRadiusX, tlRadiusX);
    final double topRadius = math.max(tlRadiusY, trRadiusY);
    final double rightRadius = math.max(trRadiusX, brRadiusX);
    final double bottomRadius = math.max(brRadiusY, blRadiusY);
    return Rect.fromLTRB(
      left + leftRadius,
      top + topRadius,
      right - rightRadius,
      bottom - bottomRadius,
    );
  }

  /// The biggest rectangle that is entirely inside the rounded rectangle and
  /// has the full width of the rounded rectangle. If the rounded rectangle does
  /// not have an axis-aligned intersection of its left and right side, the
  /// resulting [Rect] will have negative width or height.
  Rect get wideMiddleRect {
    final double topRadius = math.max(tlRadiusY, trRadiusY);
    final double bottomRadius = math.max(brRadiusY, blRadiusY);
    return Rect.fromLTRB(left, top + topRadius, right, bottom - bottomRadius);
  }

  /// The biggest rectangle that is entirely inside the rounded rectangle and
  /// has the full height of the rounded rectangle. If the rounded rectangle
  /// does not have an axis-aligned intersection of its top and bottom side, the
  /// resulting [Rect] will have negative width or height.
  Rect get tallMiddleRect {
    final double leftRadius = math.max(blRadiusX, tlRadiusX);
    final double rightRadius = math.max(trRadiusX, brRadiusX);
    return Rect.fromLTRB(left + leftRadius, top, right - rightRadius, bottom);
  }

  /// Whether this rounded rectangle encloses a non-zero area.
  /// Negative areas are considered empty.
  bool get isEmpty => left >= right || top >= bottom;

  /// Whether all coordinates of this rounded rectangle are finite.
  bool get isFinite => left.isFinite && top.isFinite && right.isFinite && bottom.isFinite;

  /// Whether this rounded rectangle is a simple rectangle with zero
  /// corner radii.
  bool get isRect {
    return (tlRadiusX == 0.0 || tlRadiusY == 0.0) &&
        (trRadiusX == 0.0 || trRadiusY == 0.0) &&
        (blRadiusX == 0.0 || blRadiusY == 0.0) &&
        (brRadiusX == 0.0 || brRadiusY == 0.0);
  }

  /// Whether this rounded rectangle has a side with no straight section.
  bool get isStadium {
    return tlRadius == trRadius &&
        trRadius == brRadius &&
        brRadius == blRadius &&
        (width <= 2.0 * tlRadiusX || height <= 2.0 * tlRadiusY);
  }

  /// Whether this rounded rectangle has no side with a straight section.
  bool get isEllipse {
    return tlRadius == trRadius &&
        trRadius == brRadius &&
        brRadius == blRadius &&
        width <= 2.0 * tlRadiusX &&
        height <= 2.0 * tlRadiusY;
  }

  /// Whether this rounded rectangle would draw as a circle.
  bool get isCircle => width == height && isEllipse;

  /// The lesser of the magnitudes of the [width] and the [height] of this
  /// rounded rectangle.
  double get shortestSide => math.min(width.abs(), height.abs());

  /// The greater of the magnitudes of the [width] and the [height] of this
  /// rounded rectangle.
  double get longestSide => math.max(width.abs(), height.abs());

  /// Whether any of the dimensions are `NaN`.
  bool get hasNaN =>
      left.isNaN ||
      top.isNaN ||
      right.isNaN ||
      bottom.isNaN ||
      trRadiusX.isNaN ||
      trRadiusY.isNaN ||
      tlRadiusX.isNaN ||
      tlRadiusY.isNaN ||
      brRadiusX.isNaN ||
      brRadiusY.isNaN ||
      blRadiusX.isNaN ||
      blRadiusY.isNaN;

  /// The offset to the point halfway between the left and right and the top and
  /// bottom edges of this rectangle.
  Offset get center => Offset(left + width / 2.0, top + height / 2.0);

  // Returns the minimum between min and scale to which radius1 and radius2
  // should be scaled with in order not to exceed the limit.
  double _getMin(double min, double radius1, double radius2, double limit) {
    final double sum = radius1 + radius2;
    if (sum > limit && sum != 0.0) {
      return math.min(min, limit / sum);
    }
    return min;
  }

  /// Scales all radii so that on each side their sum will not exceed the size
  /// of the width/height.
  ///
  /// Skia already handles RRects with radii that are too large in this way.
  /// Therefore, this method is only needed for use cases of [RRect] or
  /// [RSuperellipse] that require the appropriately scaled radii values.
  ///
  /// See the [Skia scaling implementation](https://github.com/google/skia/blob/main/src/core/SkRRect.cpp)
  /// for more details.
  T scaleRadii() {
    double scale = 1.0;
    scale = _getMin(scale, blRadiusY, tlRadiusY, height);
    scale = _getMin(scale, tlRadiusX, trRadiusX, width);
    scale = _getMin(scale, trRadiusY, brRadiusY, height);
    scale = _getMin(scale, brRadiusX, blRadiusX, width);
    assert(scale >= 0);

    if (scale < 1.0) {
      return _create(
        top: top,
        left: left,
        right: right,
        bottom: bottom,
        tlRadiusX: tlRadiusX * scale,
        tlRadiusY: tlRadiusY * scale,
        trRadiusX: trRadiusX * scale,
        trRadiusY: trRadiusY * scale,
        blRadiusX: blRadiusX * scale,
        blRadiusY: blRadiusY * scale,
        brRadiusX: brRadiusX * scale,
        brRadiusY: brRadiusY * scale,
      );
    }

    return _create(
      top: top,
      left: left,
      right: right,
      bottom: bottom,
      tlRadiusX: tlRadiusX,
      tlRadiusY: tlRadiusY,
      trRadiusX: trRadiusX,
      trRadiusY: trRadiusY,
      blRadiusX: blRadiusX,
      blRadiusY: blRadiusY,
      brRadiusX: brRadiusX,
      brRadiusY: brRadiusY,
    );
  }

  // Linearly interpolate between this object and another of the same shape.
  T _lerpTo(T? b, double t) {
    assert(runtimeType == T);
    if (b == null) {
      final double k = 1.0 - t;
      return _create(
        left: left * k,
        top: top * k,
        right: right * k,
        bottom: bottom * k,
        tlRadiusX: math.max(0, tlRadiusX * k),
        tlRadiusY: math.max(0, tlRadiusY * k),
        trRadiusX: math.max(0, trRadiusX * k),
        trRadiusY: math.max(0, trRadiusY * k),
        brRadiusX: math.max(0, brRadiusX * k),
        brRadiusY: math.max(0, brRadiusY * k),
        blRadiusX: math.max(0, blRadiusX * k),
        blRadiusY: math.max(0, blRadiusY * k),
      );
    } else {
      return _create(
        left: _lerpDouble(left, b.left, t),
        top: _lerpDouble(top, b.top, t),
        right: _lerpDouble(right, b.right, t),
        bottom: _lerpDouble(bottom, b.bottom, t),
        tlRadiusX: math.max(0, _lerpDouble(tlRadiusX, b.tlRadiusX, t)),
        tlRadiusY: math.max(0, _lerpDouble(tlRadiusY, b.tlRadiusY, t)),
        trRadiusX: math.max(0, _lerpDouble(trRadiusX, b.trRadiusX, t)),
        trRadiusY: math.max(0, _lerpDouble(trRadiusY, b.trRadiusY, t)),
        brRadiusX: math.max(0, _lerpDouble(brRadiusX, b.brRadiusX, t)),
        brRadiusY: math.max(0, _lerpDouble(brRadiusY, b.brRadiusY, t)),
        blRadiusX: math.max(0, _lerpDouble(blRadiusX, b.blRadiusX, t)),
        blRadiusY: math.max(0, _lerpDouble(blRadiusY, b.blRadiusY, t)),
      );
    }
  }

  @override
  bool operator ==(Object other) {
    if (identical(this, other)) {
      return true;
    }
    if (runtimeType != other.runtimeType) {
      return false;
    }
    return other is _RRectLike &&
        other.left == left &&
        other.top == top &&
        other.right == right &&
        other.bottom == bottom &&
        other.tlRadiusX == tlRadiusX &&
        other.tlRadiusY == tlRadiusY &&
        other.trRadiusX == trRadiusX &&
        other.trRadiusY == trRadiusY &&
        other.blRadiusX == blRadiusX &&
        other.blRadiusY == blRadiusY &&
        other.brRadiusX == brRadiusX &&
        other.brRadiusY == brRadiusY;
  }

  @override
  int get hashCode => Object.hash(
    left,
    top,
    right,
    bottom,
    tlRadiusX,
    tlRadiusY,
    trRadiusX,
    trRadiusY,
    blRadiusX,
    blRadiusY,
    brRadiusX,
    brRadiusY,
  );

  String _toString({required String className}) {
    final String rect =
        '${left.toStringAsFixed(1)}, '
        '${top.toStringAsFixed(1)}, '
        '${right.toStringAsFixed(1)}, '
        '${bottom.toStringAsFixed(1)}';
    if (tlRadius == trRadius && trRadius == brRadius && brRadius == blRadius) {
      if (tlRadius.x == tlRadius.y) {
        return '$className.fromLTRBR($rect, ${tlRadius.x.toStringAsFixed(1)})';
      }
      return '$className.fromLTRBXY($rect, ${tlRadius.x.toStringAsFixed(1)}, ${tlRadius.y.toStringAsFixed(1)})';
    }
    return '$className.fromLTRBAndCorners('
        '$rect, '
        'topLeft: $tlRadius, '
        'topRight: $trRadius, '
        'bottomRight: $brRadius, '
        'bottomLeft: $blRadius'
        ')';
  }
}

/// An immutable rounded rectangle with the custom radii for all four corners.
class RRect extends _RRectLike<RRect> {
  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and the same radii along its horizontal axis and its vertical axis.
  ///
  /// Will assert in debug mode if `radiusX` or `radiusY` are negative.
  const RRect.fromLTRBXY(
    double left,
    double top,
    double right,
    double bottom,
    double radiusX,
    double radiusY,
  ) : this._raw(
        top: top,
        left: left,
        right: right,
        bottom: bottom,
        tlRadiusX: radiusX,
        tlRadiusY: radiusY,
        trRadiusX: radiusX,
        trRadiusY: radiusY,
        blRadiusX: radiusX,
        blRadiusY: radiusY,
        brRadiusX: radiusX,
        brRadiusY: radiusY,
      );

  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and the same radius in each corner.
  ///
  /// Will assert in debug mode if the `radius` is negative in either x or y.
  RRect.fromLTRBR(double left, double top, double right, double bottom, Radius radius)
    : this._raw(
        top: top,
        left: left,
        right: right,
        bottom: bottom,
        tlRadiusX: radius.x,
        tlRadiusY: radius.y,
        trRadiusX: radius.x,
        trRadiusY: radius.y,
        blRadiusX: radius.x,
        blRadiusY: radius.y,
        brRadiusX: radius.x,
        brRadiusY: radius.y,
      );

  /// Construct a rounded rectangle from its bounding box and the same radii
  /// along its horizontal axis and its vertical axis.
  ///
  /// Will assert in debug mode if `radiusX` or `radiusY` are negative.
  RRect.fromRectXY(Rect rect, double radiusX, double radiusY)
    : this._raw(
        top: rect.top,
        left: rect.left,
        right: rect.right,
        bottom: rect.bottom,
        tlRadiusX: radiusX,
        tlRadiusY: radiusY,
        trRadiusX: radiusX,
        trRadiusY: radiusY,
        blRadiusX: radiusX,
        blRadiusY: radiusY,
        brRadiusX: radiusX,
        brRadiusY: radiusY,
      );

  /// Construct a rounded rectangle from its bounding box and a radius that is
  /// the same in each corner.
  ///
  /// Will assert in debug mode if the `radius` is negative in either x or y.
  RRect.fromRectAndRadius(Rect rect, Radius radius)
    : this._raw(
        top: rect.top,
        left: rect.left,
        right: rect.right,
        bottom: rect.bottom,
        tlRadiusX: radius.x,
        tlRadiusY: radius.y,
        trRadiusX: radius.x,
        trRadiusY: radius.y,
        blRadiusX: radius.x,
        blRadiusY: radius.y,
        brRadiusX: radius.x,
        brRadiusY: radius.y,
      );

  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and topLeft, topRight, bottomRight, and bottomLeft radii.
  ///
  /// The corner radii default to [Radius.zero], i.e. right-angled corners. Will
  /// assert in debug mode if any of the radii are negative in either x or y.
  RRect.fromLTRBAndCorners(
    double left,
    double top,
    double right,
    double bottom, {
    Radius topLeft = Radius.zero,
    Radius topRight = Radius.zero,
    Radius bottomRight = Radius.zero,
    Radius bottomLeft = Radius.zero,
  }) : this._raw(
         top: top,
         left: left,
         right: right,
         bottom: bottom,
         tlRadiusX: topLeft.x,
         tlRadiusY: topLeft.y,
         trRadiusX: topRight.x,
         trRadiusY: topRight.y,
         blRadiusX: bottomLeft.x,
         blRadiusY: bottomLeft.y,
         brRadiusX: bottomRight.x,
         brRadiusY: bottomRight.y,
       );

  /// Construct a rounded rectangle from its bounding box and topLeft,
  /// topRight, bottomRight, and bottomLeft radii.
  ///
  /// The corner radii default to [Radius.zero], i.e. right-angled corners. Will
  /// assert in debug mode if any of the radii are negative in either x or y.
  RRect.fromRectAndCorners(
    Rect rect, {
    Radius topLeft = Radius.zero,
    Radius topRight = Radius.zero,
    Radius bottomRight = Radius.zero,
    Radius bottomLeft = Radius.zero,
  }) : this._raw(
         top: rect.top,
         left: rect.left,
         right: rect.right,
         bottom: rect.bottom,
         tlRadiusX: topLeft.x,
         tlRadiusY: topLeft.y,
         trRadiusX: topRight.x,
         trRadiusY: topRight.y,
         blRadiusX: bottomLeft.x,
         blRadiusY: bottomLeft.y,
         brRadiusX: bottomRight.x,
         brRadiusY: bottomRight.y,
       );

  const RRect._raw({
    super.left = 0.0,
    super.top = 0.0,
    super.right = 0.0,
    super.bottom = 0.0,
    super.tlRadiusX = 0.0,
    super.tlRadiusY = 0.0,
    super.trRadiusX = 0.0,
    super.trRadiusY = 0.0,
    super.brRadiusX = 0.0,
    super.brRadiusY = 0.0,
    super.blRadiusX = 0.0,
    super.blRadiusY = 0.0,
  });

  @override
  RRect _create({
    required double left,
    required double top,
    required double right,
    required double bottom,
    required double tlRadiusX,
    required double tlRadiusY,
    required double trRadiusX,
    required double trRadiusY,
    required double brRadiusX,
    required double brRadiusY,
    required double blRadiusX,
    required double blRadiusY,
  }) => RRect._raw(
    top: top,
    left: left,
    right: right,
    bottom: bottom,
    tlRadiusX: tlRadiusX,
    tlRadiusY: tlRadiusY,
    trRadiusX: trRadiusX,
    trRadiusY: trRadiusY,
    blRadiusX: blRadiusX,
    blRadiusY: blRadiusY,
    brRadiusX: brRadiusX,
    brRadiusY: brRadiusY,
  );

  Float32List _getValue32() {
    final Float32List result = Float32List(12);
    result[0] = left;
    result[1] = top;
    result[2] = right;
    result[3] = bottom;
    result[4] = tlRadiusX;
    result[5] = tlRadiusY;
    result[6] = trRadiusX;
    result[7] = trRadiusY;
    result[8] = brRadiusX;
    result[9] = brRadiusY;
    result[10] = blRadiusX;
    result[11] = blRadiusY;
    return result;
  }

  /// A rounded rectangle with all the values set to zero.
  static const RRect zero = RRect._raw();

  /// Whether the point specified by the given offset (which is assumed to be
  /// relative to the origin) lies inside the rounded rectangle.
  ///
  /// This method may allocate (and cache) a copy of the object with normalized
  /// radii the first time it is called on a particular [RRect] instance. When
  /// using this method, prefer to reuse existing [RRect]s rather than
  /// recreating the object each time.
  bool contains(Offset point) {
    if (point.dx < left || point.dx >= right || point.dy < top || point.dy >= bottom) {
      return false;
    } // outside bounding box

    final RRect scaled = scaleRadii();

    double x;
    double y;
    double radiusX;
    double radiusY;
    // check whether point is in one of the rounded corner areas
    // x, y -> translate to ellipse center
    if (point.dx < left + scaled.tlRadiusX && point.dy < top + scaled.tlRadiusY) {
      x = point.dx - left - scaled.tlRadiusX;
      y = point.dy - top - scaled.tlRadiusY;
      radiusX = scaled.tlRadiusX;
      radiusY = scaled.tlRadiusY;
    } else if (point.dx > right - scaled.trRadiusX && point.dy < top + scaled.trRadiusY) {
      x = point.dx - right + scaled.trRadiusX;
      y = point.dy - top - scaled.trRadiusY;
      radiusX = scaled.trRadiusX;
      radiusY = scaled.trRadiusY;
    } else if (point.dx > right - scaled.brRadiusX && point.dy > bottom - scaled.brRadiusY) {
      x = point.dx - right + scaled.brRadiusX;
      y = point.dy - bottom + scaled.brRadiusY;
      radiusX = scaled.brRadiusX;
      radiusY = scaled.brRadiusY;
    } else if (point.dx < left + scaled.blRadiusX && point.dy > bottom - scaled.blRadiusY) {
      x = point.dx - left - scaled.blRadiusX;
      y = point.dy - bottom + scaled.blRadiusY;
      radiusX = scaled.blRadiusX;
      radiusY = scaled.blRadiusY;
    } else {
      return true; // inside and not within the rounded corner area
    }

    x = x / radiusX;
    y = y / radiusY;
    // check if the point is outside the unit circle
    if (x * x + y * y > 1.0) {
      return false;
    }
    return true;
  }

  /// Linearly interpolate between two rounded rectangles.
  ///
  /// If either is null, this function substitutes [RRect.zero] instead.
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static RRect? lerp(RRect? a, RRect? b, double t) {
    if (a == null) {
      if (b == null) {
        return null;
      }
      return b._lerpTo(null, 1 - t);
    }
    return a._lerpTo(b, t);
  }

  @override
  String toString() {
    return _toString(className: 'RRect');
  }
}

/// An immutable rounded superellipse.
///
/// A rounded superellipse (not to be confused with a standard superellipse) is
/// a shape formed by replacing the four curved corners of a superellipse with
/// circular arcs. A (standard) superellipse follows the formula x^n + y^n =
/// a^n, and while n > 2 gives it rounded corners, they tend to be too sharp and
/// pronounced.  Replacing them with circular arcs makes the shape feel softer
/// and more natural.
///
/// Visually, a rounded superellipse looks similar to a typical rounded rectangle
/// ([RRect]) but with smoother transitions between the straight edges and
/// corners. It closely matches the `RoundedRectangle` shape in SwiftUI with the
/// `.continuous` corner style.
class RSuperellipse extends _RRectLike<RSuperellipse> {
  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and the same radii along its horizontal axis and its vertical axis.
  ///
  /// Will assert in debug mode if `radiusX` or `radiusY` are negative.
  const RSuperellipse.fromLTRBXY(
    double left,
    double top,
    double right,
    double bottom,
    double radiusX,
    double radiusY,
  ) : this._raw(
        top: top,
        left: left,
        right: right,
        bottom: bottom,
        tlRadiusX: radiusX,
        tlRadiusY: radiusY,
        trRadiusX: radiusX,
        trRadiusY: radiusY,
        blRadiusX: radiusX,
        blRadiusY: radiusY,
        brRadiusX: radiusX,
        brRadiusY: radiusY,
      );

  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and the same radius in each corner.
  ///
  /// Will assert in debug mode if the `radius` is negative in either x or y.
  RSuperellipse.fromLTRBR(double left, double top, double right, double bottom, Radius radius)
    : this._raw(
        top: top,
        left: left,
        right: right,
        bottom: bottom,
        tlRadiusX: radius.x,
        tlRadiusY: radius.y,
        trRadiusX: radius.x,
        trRadiusY: radius.y,
        blRadiusX: radius.x,
        blRadiusY: radius.y,
        brRadiusX: radius.x,
        brRadiusY: radius.y,
      );

  /// Construct a rounded rectangle from its bounding box and the same radii
  /// along its horizontal axis and its vertical axis.
  ///
  /// Will assert in debug mode if `radiusX` or `radiusY` are negative.
  RSuperellipse.fromRectXY(Rect rect, double radiusX, double radiusY)
    : this._raw(
        top: rect.top,
        left: rect.left,
        right: rect.right,
        bottom: rect.bottom,
        tlRadiusX: radiusX,
        tlRadiusY: radiusY,
        trRadiusX: radiusX,
        trRadiusY: radiusY,
        blRadiusX: radiusX,
        blRadiusY: radiusY,
        brRadiusX: radiusX,
        brRadiusY: radiusY,
      );

  /// Construct a rounded rectangle from its bounding box and a radius that is
  /// the same in each corner.
  ///
  /// Will assert in debug mode if the `radius` is negative in either x or y.
  RSuperellipse.fromRectAndRadius(Rect rect, Radius radius)
    : this._raw(
        top: rect.top,
        left: rect.left,
        right: rect.right,
        bottom: rect.bottom,
        tlRadiusX: radius.x,
        tlRadiusY: radius.y,
        trRadiusX: radius.x,
        trRadiusY: radius.y,
        blRadiusX: radius.x,
        blRadiusY: radius.y,
        brRadiusX: radius.x,
        brRadiusY: radius.y,
      );

  /// Construct a rounded rectangle from its left, top, right, and bottom edges,
  /// and topLeft, topRight, bottomRight, and bottomLeft radii.
  ///
  /// The corner radii default to [Radius.zero], i.e. right-angled corners. Will
  /// assert in debug mode if any of the radii are negative in either x or y.
  RSuperellipse.fromLTRBAndCorners(
    double left,
    double top,
    double right,
    double bottom, {
    Radius topLeft = Radius.zero,
    Radius topRight = Radius.zero,
    Radius bottomRight = Radius.zero,
    Radius bottomLeft = Radius.zero,
  }) : this._raw(
         top: top,
         left: left,
         right: right,
         bottom: bottom,
         tlRadiusX: topLeft.x,
         tlRadiusY: topLeft.y,
         trRadiusX: topRight.x,
         trRadiusY: topRight.y,
         blRadiusX: bottomLeft.x,
         blRadiusY: bottomLeft.y,
         brRadiusX: bottomRight.x,
         brRadiusY: bottomRight.y,
       );

  /// Construct a rounded rectangle from its bounding box and topLeft,
  /// topRight, bottomRight, and bottomLeft radii.
  ///
  /// The corner radii default to [Radius.zero], i.e. right-angled corners. Will
  /// assert in debug mode if any of the radii are negative in either x or y.
  RSuperellipse.fromRectAndCorners(
    Rect rect, {
    Radius topLeft = Radius.zero,
    Radius topRight = Radius.zero,
    Radius bottomRight = Radius.zero,
    Radius bottomLeft = Radius.zero,
  }) : this._raw(
         top: rect.top,
         left: rect.left,
         right: rect.right,
         bottom: rect.bottom,
         tlRadiusX: topLeft.x,
         tlRadiusY: topLeft.y,
         trRadiusX: topRight.x,
         trRadiusY: topRight.y,
         blRadiusX: bottomLeft.x,
         blRadiusY: bottomLeft.y,
         brRadiusX: bottomRight.x,
         brRadiusY: bottomRight.y,
       );

  const RSuperellipse._raw({
    super.left = 0.0,
    super.top = 0.0,
    super.right = 0.0,
    super.bottom = 0.0,
    super.tlRadiusX = 0.0,
    super.tlRadiusY = 0.0,
    super.trRadiusX = 0.0,
    super.trRadiusY = 0.0,
    super.brRadiusX = 0.0,
    super.brRadiusY = 0.0,
    super.blRadiusX = 0.0,
    super.blRadiusY = 0.0,
  });

  @override
  RSuperellipse _create({
    required double left,
    required double top,
    required double right,
    required double bottom,
    required double tlRadiusX,
    required double tlRadiusY,
    required double trRadiusX,
    required double trRadiusY,
    required double brRadiusX,
    required double brRadiusY,
    required double blRadiusX,
    required double blRadiusY,
  }) => RSuperellipse._raw(
    top: top,
    left: left,
    right: right,
    bottom: bottom,
    tlRadiusX: tlRadiusX,
    tlRadiusY: tlRadiusY,
    trRadiusX: trRadiusX,
    trRadiusY: trRadiusY,
    blRadiusX: blRadiusX,
    blRadiusY: blRadiusY,
    brRadiusX: brRadiusX,
    brRadiusY: brRadiusY,
  );

  _NativeRSuperellipse _native() {
    return _NativeRSuperellipse(this);
  }

  /// Whether the point specified by the given offset (which is assumed to be
  /// relative to the origin) lies inside the rounded superellipse.
  bool contains(Offset point) {
    return _native().contains(point);
  }

  /// A rounded rectangle with all the values set to zero.
  static const RSuperellipse zero = RSuperellipse._raw();

  /// Linearly interpolate between two rounded superellipses.
  ///
  /// If either is null, this function substitutes [RSuperellipse.zero] instead.
  ///
  /// The `t` argument represents position on the timeline, with 0.0 meaning
  /// that the interpolation has not started, returning `a` (or something
  /// equivalent to `a`), 1.0 meaning that the interpolation has finished,
  /// returning `b` (or something equivalent to `b`), and values in between
  /// meaning that the interpolation is at the relevant point on the timeline
  /// between `a` and `b`. The interpolation can be extrapolated beyond 0.0 and
  /// 1.0, so negative values and values greater than 1.0 are valid (and can
  /// easily be generated by curves such as [Curves.elasticInOut]).
  ///
  /// Values for `t` are usually obtained from an [Animation<double>], such as
  /// an [AnimationController].
  static RSuperellipse? lerp(RSuperellipse? a, RSuperellipse? b, double t) {
    if (a == null) {
      if (b == null) {
        return null;
      }
      return b._lerpTo(null, 1 - t);
    }
    return a._lerpTo(b, t);
  }

  @override
  String toString() {
    return _toString(className: 'RSuperellipse');
  }
}

class _NativeRSuperellipse extends NativeFieldWrapperClass1 {
  _NativeRSuperellipse(RSuperellipse rsuperellipse) {
    _constructor(
      rsuperellipse.left,
      rsuperellipse.top,
      rsuperellipse.right,
      rsuperellipse.bottom,
      rsuperellipse.tlRadiusX,
      rsuperellipse.tlRadiusY,
      rsuperellipse.trRadiusX,
      rsuperellipse.trRadiusY,
      rsuperellipse.brRadiusX,
      rsuperellipse.brRadiusY,
      rsuperellipse.blRadiusX,
      rsuperellipse.blRadiusY,
    );
  }

  @Native<
    Void Function(
      Handle,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
      Double,
    )
  >(symbol: 'RSuperellipse::Create')
  external void _constructor(
    double left,
    double top,
    double right,
    double bottom,
    double tlRadiusX,
    double tlRadiusY,
    double trRadiusX,
    double trRadiusY,
    double brRadiusX,
    double brRadiusY,
    double blRadiusX,
    double blRadiusY,
  );

  bool contains(Offset point) {
    return _contains(point.dx, point.dy);
  }

  @Native<Bool Function(Pointer<Void>, Double, Double)>(
    symbol: 'RSuperellipse::contains',
    isLeaf: true,
  )
  external bool _contains(double x, double y);
}

/// A transform consisting of a translation, a rotation, and a uniform scale.
///
/// Used by [Canvas.drawAtlas]. This is a more efficient way to represent these
/// simple transformations than a full matrix.
// Modeled after Impeller's RSTransform.
class RSTransform {
  /// Creates an RSTransform.
  ///
  /// An [RSTransform] expresses the combination of a translation, a rotation
  /// around a particular point, and a scale factor.
  ///
  /// The first argument, `scos`, is the cosine of the rotation, multiplied by
  /// the scale factor.
  ///
  /// The second argument, `ssin`, is the sine of the rotation, multiplied by
  /// that same scale factor.
  ///
  /// The third argument is the x coordinate of the translation, minus the
  /// `scos` argument multiplied by the x-coordinate of the rotation point, plus
  /// the `ssin` argument multiplied by the y-coordinate of the rotation point.
  ///
  /// The fourth argument is the y coordinate of the translation, minus the `ssin`
  /// argument multiplied by the x-coordinate of the rotation point, minus the
  /// `scos` argument multiplied by the y-coordinate of the rotation point.
  ///
  /// The [RSTransform.fromComponents] method may be a simpler way to
  /// construct these values. However, if there is a way to factor out the
  /// computations of the sine and cosine of the rotation so that they can be
  /// reused over multiple calls to this constructor, it may be more efficient
  /// to directly use this constructor instead.
  RSTransform(double scos, double ssin, double tx, double ty) {
    _value
      ..[0] = scos
      ..[1] = ssin
      ..[2] = tx
      ..[3] = ty;
  }

  /// Creates an RSTransform from its individual components.
  ///
  /// The `rotation` parameter gives the rotation in radians.
  ///
  /// The `scale` parameter describes the uniform scale factor.
  ///
  /// The `anchorX` and `anchorY` parameters give the coordinate of the point
  /// around which to rotate.
  ///
  /// The `translateX` and `translateY` parameters give the coordinate of the
  /// offset by which to translate.
  ///
  /// This constructor computes the arguments of the [RSTransform.new]
  /// constructor and then defers to that constructor to actually create the
  /// object. If many [RSTransform] objects are being created and there is a way
  /// to factor out the computations of the sine and cosine of the rotation
  /// (which are computed each time this constructor is called) and reuse them
  /// over multiple [RSTransform] objects, it may be more efficient to directly
  /// use the more direct [RSTransform.new] constructor instead.
  factory RSTransform.fromComponents({
    required double rotation,
    required double scale,
    required double anchorX,
    required double anchorY,
    required double translateX,
    required double translateY,
  }) {
    final double scos = math.cos(rotation) * scale;
    final double ssin = math.sin(rotation) * scale;
    final double tx = translateX + -scos * anchorX + ssin * anchorY;
    final double ty = translateY + -ssin * anchorX - scos * anchorY;
    return RSTransform(scos, ssin, tx, ty);
  }

  final Float32List _value = Float32List(4);

  /// The cosine of the rotation multiplied by the scale factor.
  double get scos => _value[0];

  /// The sine of the rotation multiplied by that same scale factor.
  double get ssin => _value[1];

  /// The x coordinate of the translation, minus [scos] multiplied by the
  /// x-coordinate of the rotation point, plus [ssin] multiplied by the
  /// y-coordinate of the rotation point.
  double get tx => _value[2];

  /// The y coordinate of the translation, minus [ssin] multiplied by the
  /// x-coordinate of the rotation point, minus [scos] multiplied by the
  /// y-coordinate of the rotation point.
  double get ty => _value[3];
}